为啥要有LambdaRank

首先来看这么一个问题，机器学习一般都会有两个指标，一个叫做优化指标(Optimization Cost)，另一个叫做评测指标(Target Cost)，其中优化指标是训练时一直优化的目标，他一般都是需要连续可导（否则优化难度很大），另一个评测指标就是模型训练完了之后来评估这个模型的好坏。比如SVM模型的优化指标就是样本点距离分类面的距离最大化($\underset{w,b}{max} \quad \gamma$),而其评测指标一般都是准确率、F1值或者AUC等。
在信息检索领域其实也是这样，其排序的评测指标一般是NDCG、MAP、ERR等，但是这类指标都是非凸或者不连续，并无法直接进行优化，所以很多排序学习算法的优化一般都是都是Corss Entropy或者MSE。

在RankNet中优化的目标是Corss Entropy，他们是近似于Pairwise Error,但是这个评估指标并没有考虑排在靠前的文档。

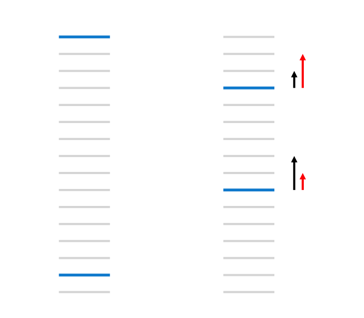
图1
如图1，每个线条表示一个文档，位置越上面表示排序越靠前，其中蓝色线条表示相关的文档，灰色则是不相关的文档，计算左侧得到的Pairwise Error为13，此时将最上面的蓝色线条下移3个位置，将下面的蓝色线条上移5个位置，则其Pairwise Error下降到了11。然而传统的排序评估指标NDCG或者ERR都是比较关心靠前的位置，类似刚刚右侧的变化并不希望出现。
而LambdaRank可以支持对这种非平滑的评估指标(比如NDCG)进行直接的优化.

LambdaRank原理

在图1右侧中，我们用$D_i$和$D_j$分别表示上下两个相关的文档，对于训练时下一次的移动中，我们更加愿意看到红色箭头的变化，因为此时$D_i$移动头部比$D_j$移动到头部明显代价更小，并且同样能减少损失函数.
对于$i << j$这种情况($D_i$排在前面)，LambdaRank将会有:
$$|\frac{\partial C}{\partial o_i}| >> |\frac{\partial C}{\partial o_j}|$$

同时，LambdaRank并不是显示对的优化函数进行求导在求最优，而是
$$\frac{\partial C}{\partial o_i} = -\lambda_i(o_1,l_1…o_n,l_n)$$，

$o_i$表示给定query下文档的打分值,$l_i$表示该文档对应的标签

可以看到这个梯度是依赖query下全部文档的分数以及其标签,这也应该是算一个ListWise的学习方法了,其中式子中带了符号表示$\lambda_i$为正数时将会在排序列表中向上移动同时会降低损失函数的值.
那么问题来了，这个$\lambda$函数该如何选呢?

在RankNet的神经网络加速算法中，其
$$\lambda_{i,j} = \frac{\partial{C}}{\partial{o_i}} = -\frac{\partial{C}}{\partial{o_j}} = -\frac{1}{1+e^{o_i-o_j}} $$

这里目标概率$\overline{P}_{i,j}=1$

LambdaRank的机智之处就是在计算$\lambda_{i,j}$的时候引入了优化指标的梯度,变成了
$$\lambda_{i,j} = -\frac{1}{1+e^{o_i-o_j}} |\Delta Z|$$
其中$\Delta Z$表示将文档$D_i$和$D_j$的位置相关调换之后重新计算得到的评估指标的差值（此时其他的文档顺序是不变的）
即可从新计算得到$\lambda_i$为:
$$\lambda_i = \sum_{j:\{i,j\} \in I} \lambda_{i,j} - \sum_{j:\{j,i\} \in I} \lambda_{i,j}$$
这个$\lambda$可以理解为上面图中的箭头方向和强度

1. 符号表示方向，正好为向上移动
2. 大小表示强度，绝对值越大，表示移动的距离越大

接下来LambdaRank具体的训练和使用方式就即可和RankNet一致了.

这个的$\Delta Z$可以替换成任何评估指标(比如NDCG、ERR)了，这样的话其实$LambdaRank$就可以变相的直接对学习排序的评估指标进行优化了，解决了之前评估指标由于是非凸无法进行优化的问题

这个具体的证明要看去原始paper了[1],是一个不是很容易理解的东西 -_-||

总结

$LambdaRank$其实是做了两个大贡献:

1. 一是对传统的RankNet提出了一个加速算法（我直接将其丢了RankNet的学习中）
2. 二是在RankNet的优化目标的基础上添加了一个基于评估指标的梯度$\Delta Z$因子，可以变相的直接对学习排序的评估指标进行优化

虽然貌似没有见一些其他工业上说明使用了该算法，但是该算法对于鼎鼎大名的LambdaMart的启发无疑是最大的。

参考

1. Schölkopf, B, Platt, J, Hofmann, T. Learning to Rank with Nonsmooth Cost Functions[C]// MIT Press, 2007:193 - 200.
2. Burges, Christopher JC. “From ranknet to lambdarank to lambdamart: An overview.” Learning 11 (2010): 23-581.
3. Li, Hang. “Learning to rank for information retrieval and natural language processing.” Synthesis Lectures on Human Language Technologies 7.3 (2014): 1-121.

---

本作品采用[知识共享署名-非商业性使用-相同方式共享 2.5]中国大陆许可协议进行许可，我的博客欢迎复制共享，但在同时，希望保留我的署名权kubiCode，并且，不得用于商业用途。如您有任何疑问或者授权方面的协商，请给我留言。